18 Difference in Differences
18.1 Introduction
One of the most popular ways to estimate the effect of a policy change is the method of difference in differences, often called “diff in diffs”. Estimation is typically a two-way panel data regression with a policy indicator as a regressor. Clustered variance estimation is generally recommended for inference.
In order to intrepret a difference in difference estimate as a policy effect there are three key conditions. First, that the estimated regression is the correct conditional expectation. In particular, this requires that all trends and interactions are properly included. Second, that the policy is exogenous it satisfies conditional independence. Third, there are no other relevant unincluded factors coincident with the policy change. If these assumptions are satisfied the difference in difference estimand is a valid causal effect.
18.2 Minimum Wage in New Jersey
The most well-known application of the difference in difference methodology is Card and Krueger (1994) who investigated the impact of New Jersey’s 1992 increase of the minimum hourly wage from
Table 18.1: Average Employment at Fast Food Restaurants
| New Jersey | Pennsylvania | Difference | |
|---|---|---|---|
| Before Increase | |||
| After Increase | |||
| Difference |
The data file CK1994 is extracted from the original Card-Krueger data set and is posted on the textbook webpage. Table
This estimate - the change in employment - could be called a difference estimator. It is the change in employment coincident with the change in policy. A difficulty in interpretation is that all employment change is attributed to the policy. It does not provide direct evidence of the counterfactual - what would have happened if the minimum wage had not been increased.
A difference in difference estimator improves on a difference estimator by comparing the change in the treatment sample with a comparable change in a control sample.
Card and Krueger selected eastern Pennsylvania for their control sample. The minimum wage was constant at
Card and Krueger surveyed a panel of 79 fast food restaurants in eastern Pennsylvania simultaneously while surveying the New Jersey restaurants. The average number of full-time equivalent employees is displayed in the second column of Table 18.1. Before the policy change the average number of employees was 23.4. After the policy change the average number was 21.1. Thus in Pennsylvania average employment decreased by
Treating Pennsylvania as a control means comparing the change in New Jersey (0.5) with that in Pennsylvnia
It is constructive to re-write the estimates from Table
Table
Indeed the coefficients can be written in terms of Table
| New Jersey | Pennsylvania | Difference | |
|---|---|---|---|
| Before Increase | |||
| After Increase | |||
| Difference |
We see that the coefficients in the regression (18.1) correspond to interpretable difference and difference in difference estimands.
Our estimate of the regression (18.1) is
The standard errors are clustered by restaurant. As expected the coefficient
Since the observations are divided into the groups State
where
which are identical to the previous regression.
Equation (18.3) is the basic difference-in-difference model. It is a two-way fixed effects regression of the response
Another common generalization is to augment the regression with controls
Many empirical studies report estimates both of the basic model and regressions with controls. For example we could augment the Card-Krueger regression to include the variable hoursopen, the number of hours a day the restaurant is open. A restaurant with longer hours will tend to have more employees.
The estimated effect is that a restaurant employs an additional
18.3 Identification
Consider the difference-in-difference equation (18.5) for
In Section
We now present sufficient conditions under which the coefficient
Theorem 18.1 Suppose the following conditions hold:
Conditional on
Then the coefficient
Condition 1 states that the outcome equals the specified linear regression model which is additively separable in the observables, individual effect, and time effect.
Condition 2 states that the two-way within transformed regressors have a non-singular design matrix. This requires that all elements of
Condition 3 is the standard exogeneity asumption for regressors in a fixed-effects model.
Condition 4 states that the treatment variable is conditionally independent of the idiosyncratic error. This is the conditional independence assumption for fixed effects regression.
To show Theorem 18.1 apply the two-way within transformation (17.65) to (18.5). We obtain
Under Condition 2 the projection coefficients
The assumption that
Furthermore, independence of
It is difficult to know if the exogeneity of
In the case of the Card-Krueger application the authors argue that the policy was exogeneous because it was adopted two years before taking effect. At the time of the passage of the legislation the economy was in an expansion but by the time of adoption the economy has slipped into recession. This suggests that it is credible to assume that the policy decision in 1990 was not affected by employment levels in 1992. Furthermore, concern about the impact of the increased minimum wage during a recession led to a serious discussion about reversing the policy, meaning that there was uncertainty about whether or not the policy would actually be enacted at the time of the first survey. It thus seems credible that employment decisions at that time were not determined in anticipation of the upcoming minimum wage increase.
The authors do not discuss, however, whether or not there were other coincident events in the New Jersey or Pennsylvania economies during 1992 which could have affected employment differentially in the two states. It seems plausible that there could have been many such coincident events. This seems to be the greatest weakness in their identification argument.
Identification (the conditions for Theorem 18.1) also requires that the regression model is correctly specified. This means that the true model is linear in the specified variables and all interactions are included. Since the basic
18.4 Multiple Units
The basic difference-in-difference model has two aggregate units (e.g. states) and two time periods. Additional information can be obtained if there are multiple units or multiple time periods. In this section we focus on the case of multiple units. There can be multiple treatment units, multiple control units, or both. In this section we suppose that the number of periods is
The basic regression model
imposes two strong restrictions. First, that all units are equally affected by time as
The Card-Krueger data set only contains observations from two states but the authors did record additional variables including the region of the state. They divided New Jersey into three regions (North, Central, and South) and eastern Pennsylvania into two regions ( 1 for northeast Philadelphia suburbs and 2 for the remainder).
Table
We can test the assumption of equal treatment effect
In contrast, when the treatment effect
A more serious problem arises if the control effect is heterogeneous. The control effect is the change in the control group. Table
In contrast, if the control effect were heterogeneous then the difference-in-difference estimation strategy is misspecified. The method relies on the ability to identify a credible control sample. Therefore if a test for equal control effects rejects the hypothesis of homogeneous control effects this should be taken as evidence against interpretation of the difference-in-difference parameter as a treatment effect.
Table 18.2: Average Employment at Fast Food Restaurants
| South NJ | Central NJ | North NJ | PA 1 | PA 2 | |
|---|---|---|---|---|---|
| Before Increase | |||||
| After Increase | |||||
| Difference |
18.5 Do Police Reduce Crime?
DiTella and Schargrodsky (2004) use a difference-in-difference approach to study the question of whether the street presence of police officers reduces car theft. Rational crime models predict that the the presence of an observable police force will reduce crime rates (at least locally) due to deterrence. The causal effect is difficult to measure, however, as police forces are not allocated exogenously, but rather are allocated in anticipation of need. A difference-in-difference estimator requires an exogenous event which changes police allocations. The innovation in DiTella-Schargrodsky was to use the police response to a terrorist attack as exogenous variation.
In July 1994 there was a horrific terrorist attack on the main Jewish center in Buenos Aires, Argentina. Within two weeks the federal government provided police protection to all Jewish and Muslim buildings in the country. DiTella and Schargrodsky (2004) hypothesized that their presence, while allocated to deter a terror or reprisal attack, would also deter other street crimes such as automobile theft locally to the deployed police. The authors collected detailed information on car thefts in selected neighborhoods of Buenos Aires for April-December 1994, resulting in a panel for 876 city blocks. They hypothesized that the terrorist attack and the government’s response were exogenous to auto thievery and is thus a valid treatment. They postulated that the deterrence effect would be strongest for any city block which contained a Jewish institution (and thus police protection). Potential car thiefs would be deterred from a burglary due to the threat of being caught. The deterrence effect was expected to weaken as the distance from the protected sites increased. The authors therefore proposed a difference-in-difference estimator based on the average number of car thefts per block, before and after the terrorist attack, and between city blocks with and without a Jewish institution. Their sample has 37 blocks with Jewish institutions (the treatment sample) and 839 blocks without an institution (the control sample).
The data file DS2004 is a slightly revised version of the author’s AER replication file and is posted on the textbook webpage.
Table 18.3: Number of Car Thefts by City Block
| Same Block | Not on Same Block | Difference | |
|---|---|---|---|
| April-June | |||
| August-December | |||
| Difference |
Table
A general way to estimate a diff-in-diff model is a regression of the form (18.3) where
The model (18.3) makes the strong assumption that the treatment effect is constant across the five treated months. We investigate this assumption in Table
| Pre-Attack | April | Same Block | Not on Same Block | Difference |
|---|---|---|---|---|
| May | ||||
| June | ||||
| Post-Attack | August | |||
| September | ||||
| October | ||||
| November | ||||
| December | ||||
months the average number per block ranges from
We can formally test the homogeneity of the treatment effect by including four dummy variables for the interactions of four post-attack months with the treatment sample and then testing the exclusion of these variables. The
The goal was to estimate the causal effect of police presence as a deterrence for crime. Let us evaluate the case for identification. It seems reasonable to treat the terrorist attack as exogenous. The government response also appears exogenous. Neither is reasonably related to the auto theft rate. We also observe that the evidence in Tables
The authors asserted the inference that police presence deters crime more broadly. This is a tenuous extension as the paper does not provide direct evidence of this claim. While it may seem reasonable we should be cautious about making generalizations without supporting evidence.
Overall, DiTella and Schargrodsky (2004) is an excellent example of a well-articulated and credibly identified difference-in-difference estimate of an important policy effect.
18.6 Trend Specification
Some applications (including the two introduced earlier in this chapter) apply to a short period of time such as one year in which case we may not expect the variables to be trended. Other applications cover many years or decades in which case the variables are likely to be trended. These trend can reflect long-term growth, business cycle effects, changing tastes, or many other features. If trends are incor- rectly specified then the model will be misspecified and the estimated policy effect will be inconsistent due to omitted variable bias. Consider the difference-in-difference equation (18.5). This model imposes the strong assumption that the trends in
One way to think about this is in terms of overidentification. For simplicity suppose there are no controls and the panel is balanced. Then there are
One generalization is to include interactions of a linear trend with a control variable. This model is
It specifies that the trend in
A broader generalization is to include unit-specific linear time trends. This model is
In this model
Estimation of model (18.6) can be done one of three ways. If
When
This is a generalized within transformation. The residuals
The relevance of the trend fixed effects
Our discussion for simplicity has focused on the case of balanced panels. The methods equally apply to unbalanced panels, using standard panel data estimation.
18.7 Do Blue Laws Affect Liquor Sales?
Historically many U.S. states prohibited or limited the sale of alcoholic beverages on Sundays. These laws are known as “blue laws”. In recent years these laws have been relaxed. Have these changes led to increased consumption of alcoholic beverages? Bernheim, Meer and Novarro (2016) investigated this question using a detailed panel on alcohol consumption and sales hours. It is possible that observed changes coincident with changes in the law might reflect underlying trends. The fact that different states changed their laws during different years allows for a difference-in-difference methodology to identify the treatment effect.
The paper focuses on distilled liquor sales though wine and beer sales are also included in their data. An abridged version of their data set BMN2016 is posted on the textbook webpage. Liquor is measured in per capita gallons of pure ethanol equivalent. The data are state-level for 47 U.S. states for the years 1970-2007, unbalanced.
The authors carefully gathered information on the allowable hours that alcohol can be sold on a Sunday. They make a distinction between off-premise sales (liquor stores, supermarkets) where consumption is off-premise, and on-premise sales (restaurants, bars) where consumption is on-premise. Let
OnHours and OffHours are the number of allowable Sunday on-premises and off-premises sale hours. UR is the state unemploment rate. OnOutFlows (OffOutFlows) is the weighted number of on(off)-premises sale hours less than neighbor states. These are added to adjust for possible cross-border transactions. The model includes both state and year fixed effects. The standard errors are clustered by state.
The estimates indicate that increased on-premise sale hours lead to a small increase in liquor sales. This is consistent with alcohol being a complementary good in social (restaurant and bar) settings. The small and insignificant coefficient on OffHours indicates that increased off-premise sale hours does not lead to an increase in liquor sales. This is consistent with rational consumers who adjust their purchases to known hours. The negative effect of the unemployment rate means that liquor sales are pro-cyclical.
The authors were concerned whether their dynamic and trend specifications were correctly specified so tried some alternative specifications and interactions. To understand the trend issue we plot in Figure
If we augment the basic model to include state-specific linear trends the estimates are as follows.
The estimated coefficient for OnHours drops to zero and becomes insignificant. The other estimates do not change meaningfully. The authors only discuss this regression in a footnote stating that adding statespecific trends “demands a great deal from the data and leaves too little variation to identify the effects of interest.” This is an unfortunate claim as actually the standard errors have decreased, not increased,
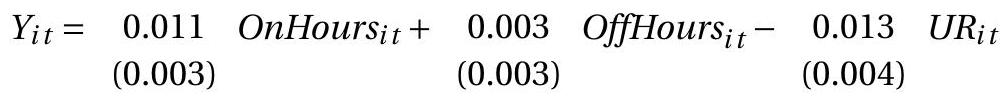
.jpg)
.jpg)
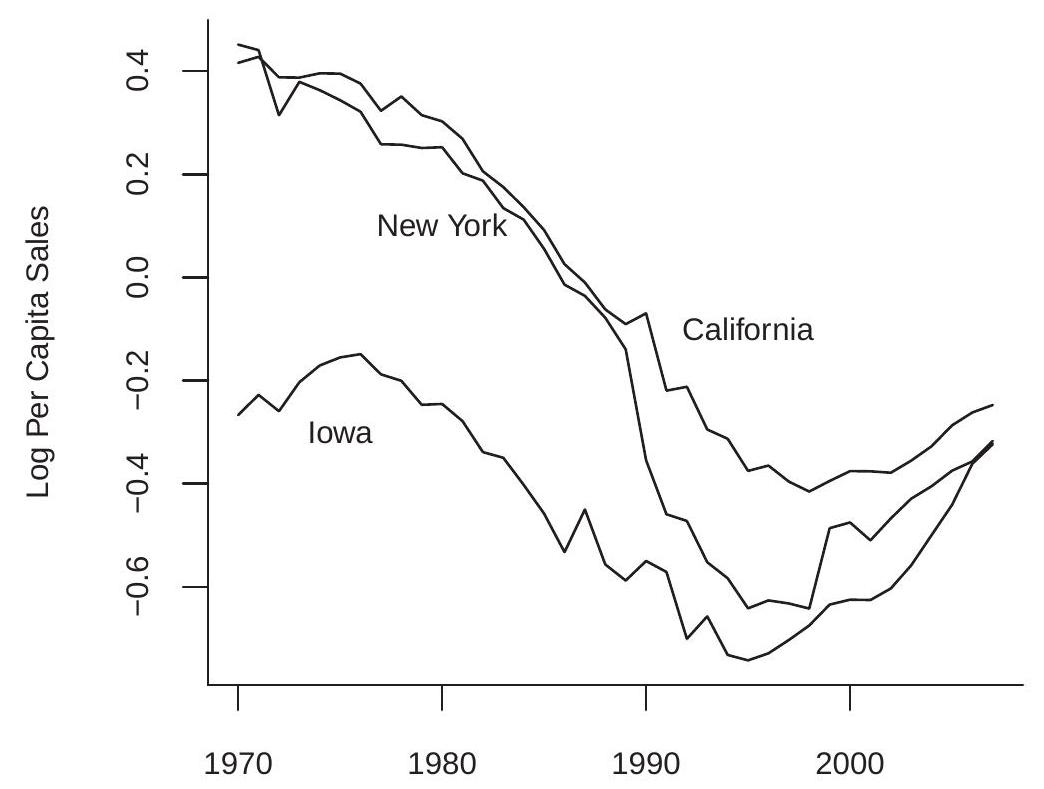
Figure 18.1: Liquor Sales by State
indicating that the effects are better identified. The trouble is that OnHours and OffHours are trended and the trends vary by state. This means that these variables are correlated with the state-trend interaction. Omitting the trend interaction induced omitted variable bias. That explains why the coefficient estimates change when the trend specification changes.
Bernheim, Meer and Novarro (2016) is an excellent example of meticulous empirical work with careful attention to detail and isolating a treatment strategy. It is also a good example of how attention to trend specification can affect results.
18.8 Check Your Code: Does Abortion Impact Crime?
In a highly-discussed paper, Donohue and Levitt (2001) used a difference-in-difference approach to develop an unusual theory. Crime rates fell dramatically throughout the United States in the 1990s. Donohue and Levitt postulated that one contributing explanation was the landmark 1973 legalization of abortion. The latter might affect the crime rate through two potential channels. First, it reduced the cohort size of young males. Second, it reduced the cohort size of young males at risk for criminal behavior. This suggests the substantial increase in abortions in the early 1970s will translate into a substantial reduction in crime 20 years later.
As you might imagine this paper was controversial on several dimensions. The paper was also meticulous in its empirical analysis, investigating the potential links using a variety of tools and differing levels of granularity. The most detailed-oriented regressions were presented at the very end of the paper where the authors exploited differences across age groups. These regressions took the form
where
Unfortunately, their estimates contained an error. In an attempt to replicate Donohue-Levitt’s work Foote and Goetz (2008) discovered that Donohue-Levitt’s computer code inadvertently omitted the stateyear interactions
Regardless of the errors and political ramifications the Donohue-Levitt paper is a very clever and creative use of the difference-in-difference method. It is unfortunate that this creative work was somewhat overshadowed by a debate over computer code.
I believe there are two important messages from this episode. First, include the appropriate controls! In the Donohue-Levitt regression they were correct to advocate for the regression which includes stateyear interactions as this allows the most precise measurement of the desired causal impact. Second, check your code! Computation errors are pervasive in applied economic work. It is very easy to make errors; it is very difficult to clean them out of lengthy code. Errors in most papers are ignored as the details receive minor attention. Important and influential papers, however, are scrutinized. If you ever are so blessed as to write a paper which receives significant attention you will find it most embarrassing if a coding error is found after publication. The solution is to be pro-active and vigilant.
18.9 Inference
Many difference-in-difference applications use highly aggregate (e.g. state level) data because they are investigating the impact of policy changes which occur at an aggregate level. It has become customary in the recent literature to use clustering methods to calculate standard errors with clustering applied at a high level of aggregation.
To understand the motivation for this choice it is useful to review the traditional argument for clustered variance estimation. Suppose that the error
as originally derived by Moulton (1990). This inflates the “usual” variance by the factor
The clustered variance estimator imposes no structure on the conditional variances and correlations within each group. It allows for arbitrary relationships. The advantage is that the resulting variance estimators are robust to a broad range of correlation structures. The disadvantage is that the estimators can be much less precise. Effectively, clustered variance estimators should be viewed as constructed from the number of groups. If you are using U.S. states as your groups (as is commonly seen in applications) then the number of groups is (at most) 51. This means that you are estimating the covariance matrix using 51 observations regardless of the number of “observations” in the sample. One implication is that if you are estimating more than 51 coefficients the sample covariance matrix estimator will not be full rank which can invalidate potentially relevant inference methods.
The case for clustered standard errors was made convincingly in an influential paper by Bertrand, Duflo, and Mullainathan (2004). These authors demonstrated their point by taking the well-known CPS dataset and then adding randomly generated regressors. They found that if non-clustered variance estimators were used then standard errors would be much too small and a researcher would inappropriately conclude that the randomly generated “variable” has a significant effect in a regression. The false rejections could be eliminated by using clustered standard errors, clustered at the state level. Based on the recommendations from this paper, researchers in economics now routinely cluster at the state level.
There are limitations, however. Take the Card-Krueger (1994) example introduced earlier. Their sample had only two states (New Jersey and Pennsylvania). If the standard errors are clustered at the state level then there are only two effective observations available for standard error calculation, which is much too few. For this application clustering at the state level is impossible. One implication might be that this casts doubts on applications involving just a handful of states. If we cannot rule out clustered dependence structures, and cannot use clustering methods due to the small number of states, then it may be inappropriate to trust the reported standard errors.
Another challenge arises when treatment
The same analysis applies to cluster-variance estimators. If there is a single treated unit then the standard clustered covariance matrix estimator will be singular. If you calculate a standard error for the sub-group mean it will be algebraically zero despite being the most imprecisely estimated coefficient. The treatment effect will have a non-zero reported standard error but it will be incorrect and highly biased towards zero. For a more detailed analysis and recommendations for inference see Conley and Taber (2011).
18.10 Exercises
Exercise 18.1 In the text it was claimed that in a balanced sample individual-level fixed effects are orthogonal to any variable demeaned at the state level.
Show this claim.
Does this claim hold in unbalanced samples?
Explain why this claim implies that the regressions
and
yield identical estimates of
Exercise 18.2 In regression (18.1) with
where
Find an algebraic expression for the least squares estimator
Show that
Is
Under which assumptions might
Exercise 18.3 Take the basic difference-in-difference model
Instead of assuming that
Hint: Review Section 17.28.
Exercise 18.4 For the specification tests of Section 18.4 explain why the regression test for homogeneous treatment effects includes only
Exercise 18.5 An economist is interested in the impact of Wisconsin’s 2011”Act 10” legislation on wages. (For background, Act 10 reduced the power of labor unions.) She computes the following statistics
| Years | Average Wage | |
|---|---|---|
| Wisconsin | ||
| Wisconsin | ||
| Minnesota | ||
| Minnesota |
Based on this information, what is her point estimate of the impact of Act 10 on average wages?
The numbers in the above table were calculated as county-level averages. (The economist was given the average wage in each county. She calculated the average for the state by taking the average across the counties.) Now suppose that she estimates the following linear regression, treating individual counties as observations.
What value of
- What value of
Exercise 18.6 Use the datafile CK1994 on the textbook webpage. Classical economics teaches that increasing the minimum wage will increase product prices. You can therefore use the Card-Krueger diffin-diff methodology to estimate the effect of the 1992 New Jersey minimum wage increase on product prices. The data file contains the variables priceentree, pricefry and pricesoda. Create the variable price as the sum of these three, indicating the cost of a typical meal.
- Some values of price are missing. Delete these observations. This will produce an unbalanced panel as price may be missing for only one of the two surveys. Balance the panel by deleting the paired observation. This can be accomplished in Stata by the commands:
drop if price
bys store: gen nperiods
keep if nperiods
Create an analog of Table
Estimate an analog of regression (18.2) with price as the dependent variable.
Estimate an analog of regression (18.4) with state fixed effects and price as the dependent variable.
Estimate an analog of regression (18.4) with restaurant fixed effects and price as the dependent variable.
Are the results of these regressions the same?
Create an analog of Table
Test for homogeneous treatment effects across regions.
Test for equal control effects across regions.
Exercise 18.7 Use the datafile DS2004 on the textbook webpage. The authors argued that an exogenous police presence would deter automobile theft. The evidence presented in the chapter showed that car theft was reduced for city blocks which received police protection. Does this deterrence effect extend beyond the same block? The dataset has the dummy variable oneblock which indicates if the city block is one block away from a protected institution.
Calculate an analog of Table
Estimate a regression with block and month fixed effects which includes two treatment variables: for city blocks which are on the same block as a protected institution, and for city blocks which are one block away, both interacted with a post-July dummy. Exclude observations for July. (c) Comment on your findings. Does the deterrence effect extend beyond the same city block?
Exercise 18.8 Use the datafile BMN2016 on the textbook webpage. The authors report results for liquor sales. The data file contains the same information for beer and wine sales. For either beer or wine sales, estimate diff-in-diff models similar to (18.7) and (18.8) and interpret your results. Some relevant variables are